折线图是一种非常常用的图表类型。有时,我们为了使其在视觉上更加柔和美观,会将折线进行光滑处理,得到曲线图。
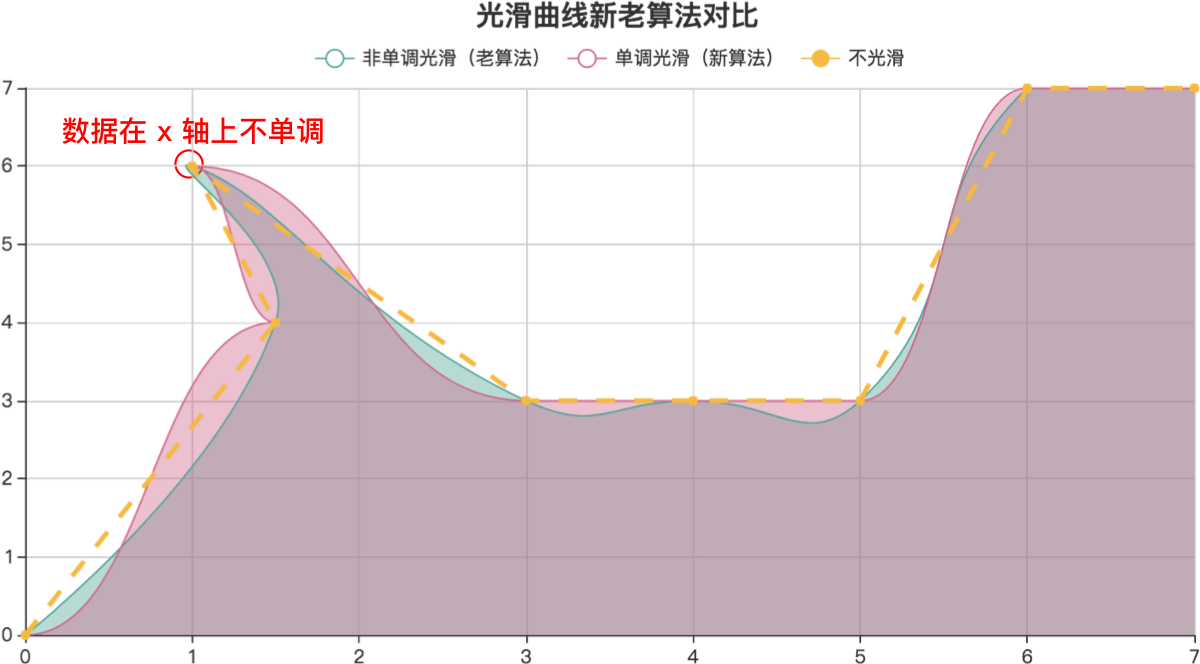
之前我在使用 ECharts 的时候,直观上觉得它的曲线效果有点奇怪。于是对其进行了优化,也相应地了解到了光滑曲线的算法,将会在本文中和大家一起探讨。下图是 ECharts 新老光滑算法的对比,其中黄色的虚线是初始数据组成的折线段,绿色是之前的光滑结果,红色是我这次修改后的光滑结果。
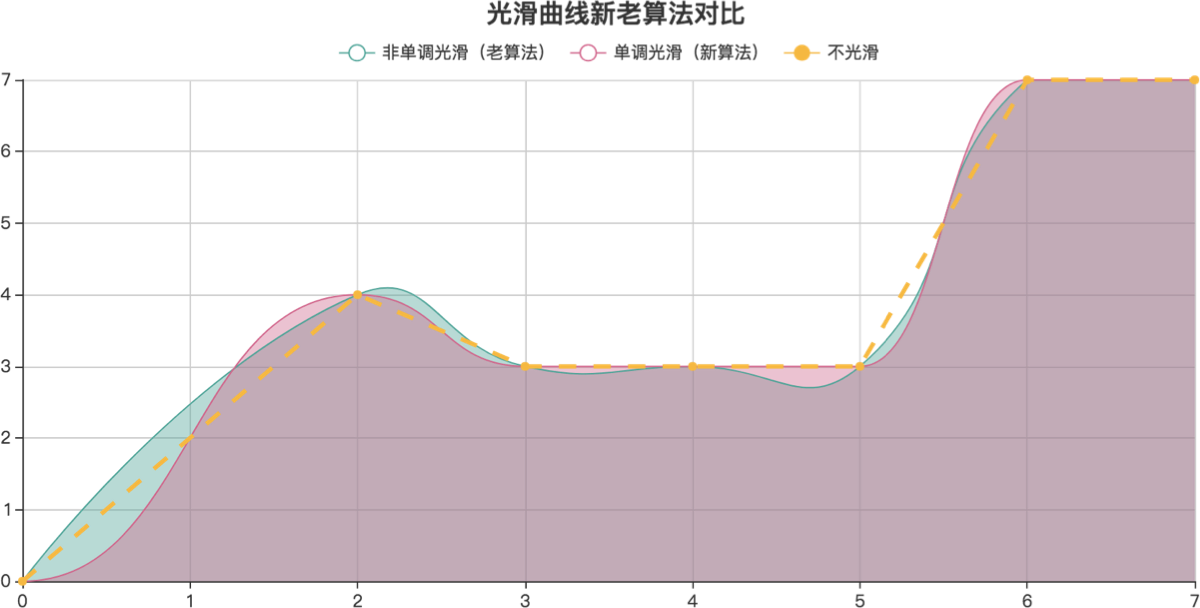
那么,为什么我会直观上觉得原先的光滑结果有问题呢?以下是几点不合理的情况:
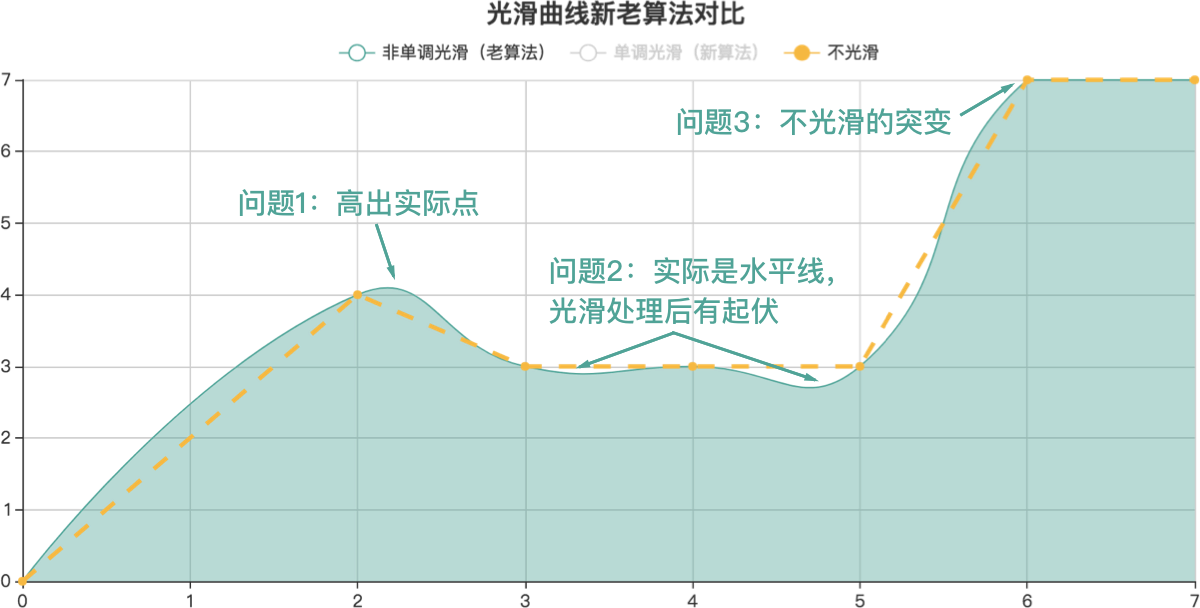
曲线的平滑处理是使用贝塞尔曲线实现的,简单地说,我们可以通过贝塞尔曲线的控制点位置,决定曲线的切线方向。如下图所示,我们可以通过红色线段的三个端点(中间的一个是经过数据点的,两边的两个端点是贝塞尔曲线的两个控制点)觉得曲线的切线。当这三个点在同一直线上时,曲线就是光滑的(也就是“可导”的)。
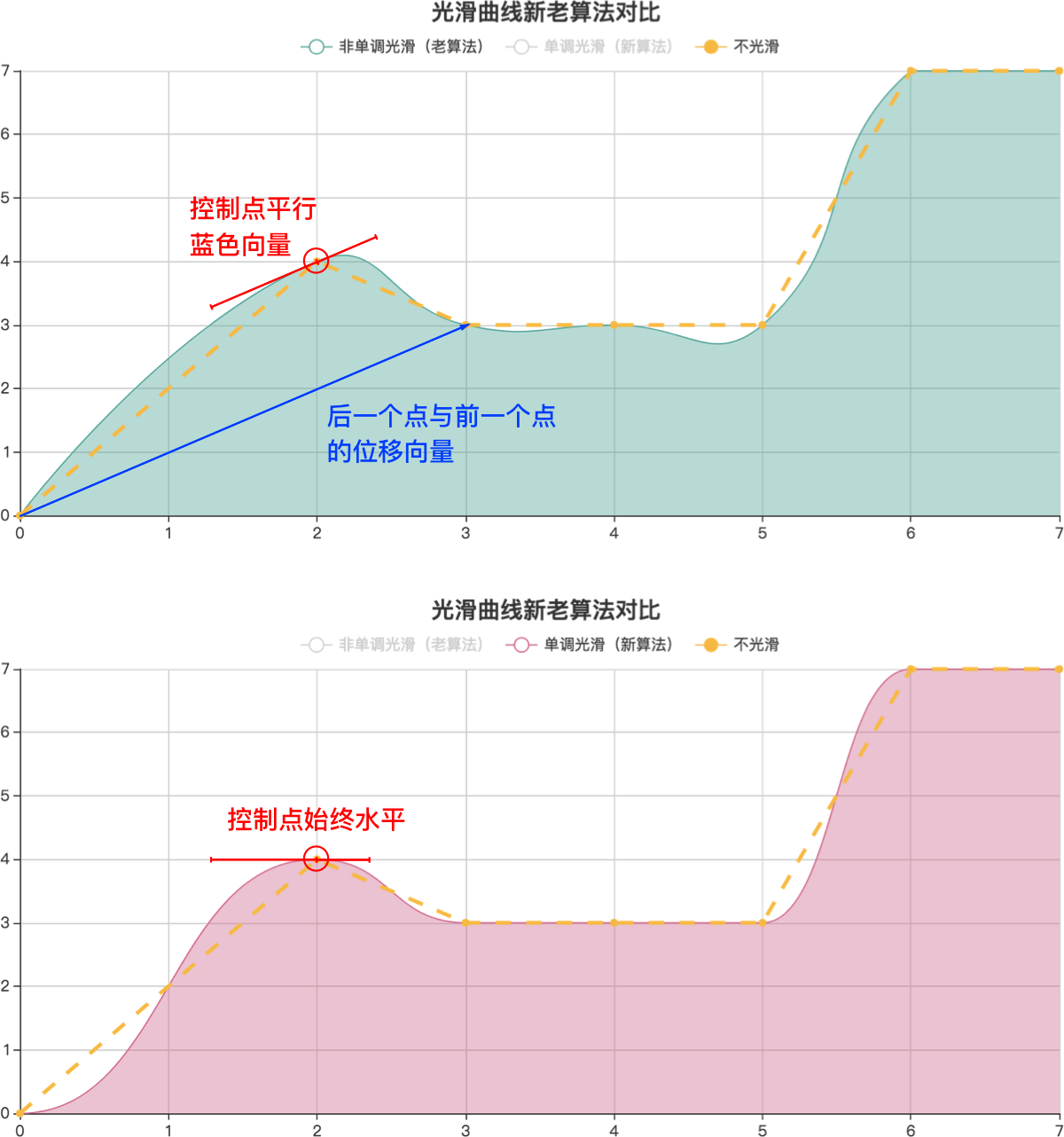
原先的算法通过计算数据点前后两个点组成的向量,使得曲线在数据点处与该向量相切。这是一种常见的图形学处理简化折线段的算法,用在光滑折线段时,能够很好地减少曲线的抖动。但是,它的问题也是显而易见的。
而在新算法中,控制点组成的线段始终是水平方向(或竖直方向),确保了控制点不会高于或低于拐点处的数据,因此光滑的结果也更符合直观期望。
但是新算法也有缺陷,当数据不是单调递增的时候,光滑的结果就不太理想,如下图所示。原因是,这时候两个控制点都在数据点的同一边。这时候,ECharts 会使用旧算法进行光滑处理。